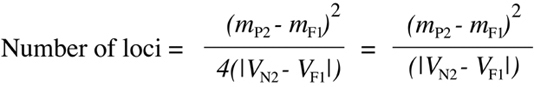
Most of the phenotypic characteristics that distinguish different individuals within a natural population are not of the all or none variety associated with laboratory-bred mouse mutations like albino, non-agouti, brown, quaking, Kinky tail, and hundreds of others. On the contrary, easily visible human traits such as skin color, wavy hair, and height, as well as hidden traits such as blood pressure, musical talent, longevity, and many others each vary over a continuous range of phenotypes. These are "quantitative traits," so-called because their expression in any single individual can only be described numerically based on the results of an appropriate form of measurement. Quantitative traits are also called continuous traits, and they stand in contrast to qualitative, or discontinuous, traits that are expressed in the form of distinct phenotypes chosen from a discrete set.
Continuous variation in the expression of a trait can be due to both genetic and non-genetic factors. Non-genetic factors can be either environmental (in the broadest definition of the term) or a matter of chance. In mice, it is relatively straightforward to separate genetic from non-genetic contributions through the analysis and comparison of animals within and between inbred strains. Variation in expression among individual members of an inbred strain must be caused by non-genetic factors. Furthermore, if one is convinced that all individuals are maintained under identical environmental conditions, then existing variation is likely to be the result of chance alone.
Geneticists are, obviously, most interested in the genetic contribution to a quantitative trait. A genetic contribution cannot be demonstrated by looking at individuals from a single inbred strain alone. Rather, a comparison of expression levels must be made on sets of animals from two different inbred strains (Figure 9.18). The statistical approach described in Appendix D2 can be used to determine formally whether two strains differ significantly in the expression of the quantitative trait. If a significant strain-specific difference is demonstrated, and all other variables have been controlled for, it becomes possible to attribute the observed difference in quantitative expression to allelic differences that distinguish the two strains.
In practice, a quantitative trait is most amenable to genetic analysis in mice and other experimental organisms with a pair of inbred strains that show non-overlapping distributions in measured levels of expression among at least 20 members of each group (Figure 9.18). Although a significant strain-specific difference can be demonstrated under much less stringent criteria (as described in Appendix D2), it becomes more and more difficult to ferret out the quantitative trait loci (QTLs) involved as the possibility of phenotypic overlap increases.
The appearance of a quantitative trait usually signifies the involvement of multiple genetic loci, although this need not be the case. In particular, a single polymorphic locus with multiple, differentially expressed alleles can give rise to continuous variation within a natural population. There may also be some instances where the expression of a quantitative trait is controlled by a mutant allele at a single locus with a high degree of variable expressivity (Asada et al., 1994). However, if a single locus is responsible for the entire genetic contribution to a quantiative trait difference between two inbred strains, this would most likely become apparent in the second generation of either an outcross-backcross or outcross-intercross breeding protocol. In the first instance, half the N2 animals will be identical to the F1 parent, and the other half will be identical to the inbred backcross parent at the critical locus as illustrated in the top panel of Figure 9.19. The result would be a discontinuous distribution of phenotypes that fall into two equally populated classes with separable distributions that parallel those found for each of the first-generation parents. With the intercross protocol, F2 animals will be distributed among three classes (in a 1:2:1 ratio) that will parallel the phenotypic distributions found among one parental strain, the F1 hybrid, and the second parental strain.
If a significant number of second-generation animals are found to express phenotypes intermediate to those found in the parental strains and F1 hybrid, 97 it is most likely that multiple genetic differences between the progenitor strains are responsible as illustrated in the lower panels of Figure 9.19. The term polygenic is used to describe traits that are controlled by multiple genes, each of which has a significant impact on expression. The term multifactorial is also used to describe such traits, but is more broadly defined to include those traits controlled by a combination of at least one genetic factor with one or more environmental factors.
Not all polygenic traits are quantitative traits. A second polygenic class consists of those traits associated with a discrete phenotype that requires particular alleles at multiple loci for its expression. Polygenic traits of this type can be classified and analyzed with breeding protocols that are the same as those used for quantiative traits. For example, suppose strain DBA shows hypersensitivity to loud noises with 100% penetrance while neither strain B6 nor F1 hybrid animals show any sensitivity. This result would indicate that hypersensitivity is recessive. Further analysis would proceed by backcrossing the F1 animals to the homozygous recessive DBA parent. If instead, the DBA trait was expressed in a dominant manner, the backcross would be made to the homozygous recessive B6 parent. In either case, backcross offspring would be typed for hypersensitivity. If 25% or less of the backcross animals expressed the trait while all of the others were normal, this would provide evidence for the requirement of at least two DBA genes to allow phenotypic expression of a discontinuous trait.
It is important to mention that more complex scenarios are possible and likely to be the rule, rather than the exception. In particular, different members of the gene set involved in the expression of a trait may differ in their relative contribution to the trait; they may behave differently relative to their corresponding wild-type allele with some showing complete dominance or recessiveness, and others showing varying degrees of partial or semi-dominance; and they may be involved in additive interactions, associative interactions or both. In some instances, a discrete trait may become quantitative upon outcrossing, or it may exhibit a threshold effect where the probability of expression in N2 offspring increases with an increasing number of critical genes from the affected parental strain. The strategy described in the next section for the analysis of polygenic traits is a general one which should be applicable to all of these situations. However, it is almost always true that the greater the genetic complexity, the larger the number of animals that will have to be bred and analzyed to obtain the same degree of genetic resolution.
Whenever viability and fecundity are not a problem, it is much more efficient to analyze complex genetic traits through a backcross rather than an intercross. This is because each backcross animal will have one of only two genotypes at each locus. In contrast, offspring from an intercross can have one of three genotypes at each locus, which can combine into many more permutations with a set of multiple unlinked, but interacting, loci. Consider the situation where three loci are involved. With the backcross, all offspring will have one of (1/2)3 = 8 different genotypes, whereas in the intercross, offspring can have one of (1/3)3 = 27 different genotypes. Furthermore, as described below, the most efficient initial method for the analysis of polygenic traits is based on the collection and analysis of DNA from only those animals that express the most extreme forms of the phenotype since these animals are most likely to be homozygous for all of the involved genes. If three genes are involved, ~12.5% of the N2 animals will have a genotype equivalent to the backcross parent and an equivalent proportion will be identical to the F1 parent. However, in offspring from an intercross, only 1.6% will be expected to have a genotype equivalent to that of each parental strain. Finally, as discussed in Section 9.4.3, when marker data are finally obtained, their compilation and analysis is much easier for a backcross than an intercross.
Before embarking on a detailed mapping project, it is useful to derive an estimate of the number of segregating genes involved in the expression of the trait under analysis. In complex cases of inheritance, the derivation of such an estimate will not be possible. However, an estimate can be made in two simple situations. The first is that of a discrete phenotype whose expression shows an absolute requirement for alleles at multiple unlinked loci from the affected parent. With a sufficient number of backcross animals, an estimation of gene number in this situation is trivial because the expression of the variant phentotype is absolutely correlated with the presence of a parental strain genotype at all involved loci. The probability of this occurrence is (0.5)n where n is the total number of loci required for expression. Thus, if the observed proportion of affected animals is ~25%, this would imply the action of two required genes, at ~12.5%, the prediction would be three genes, at ~6.25%, the prediction would be four genes, and so on. With these numbers, it is easy to see that each additional locus will require a doubling in the total number of backcross animals that must be phenotyped to obtain the same number of affected animals for genotyping.
In the case of quantitative traits, it is also possible to estimate gene number if one makes the simplifying assumption that all involved genes are
unlinked and active in a strictly semidominant manner with an equivalent contribution to the phenotype. In this situation, one can use a modified form
of a formula derived by
Wright (1952) for an intercross analysis and known as "Wright's polygene estimate":
where mP2, mN2 and mF1 are the mean values of expression of the backcross parent, the N2 population and the F1 hybrid respectively, and VN2 and VF1 are the computed variances 98 for the N2 and F1 populations respectively. The two forms of the equation shown here are mathematically equivalent so long as the mean value of the N2 population is halfway between the means of the F1 and the backcross parent. One can see the logic behind this equation by considering the probability that a backcross animal will show an extreme phenotype associated with one of its parents. From Figure 9.19, one can see the proportion of genotypes equivalent to either parent drop by a factor of two with each successive increase in locus number from one to two to three. As a consequence, the variance in the complete N2 generation (shown in the right panels of Figure 9.19) will also drop as values tend to cluster more around the mean. As the N2 variance goes down, the denominator of Equation 9.11 will decrease as well. It is important to realize that Equation 9.10 will only provide a very rough, minimum estimate of locus number because it is unlikely that all of the assumptions that went into the use of the equation will hold true in a real biological situation.
The first step in polygenic analysis is the same as the first step in mapping a single phenotypically defined locus — the choice of two parental strains (Section 9.4.2). Unlike the situation with single locus studies, the two parental strains to be choosen for polygenic analysis must be inbred; if not, unexpected and uninterpretable genetic complications could arise. The most important consideration in the choice of parental strains is that they should show the greatest difference possible in the expression of the trait under analysis. Other considerations are the same as those discussed in Section 9.4.2 with the caveat that an investigator may want to avoid interspecific, and perhaps intersubspecific, crosses because of the possibility that "abnormal" admixtures of alleles may not function together as they would in a normal offspring from either breeding group.
Upon choosing two inbred parental strains (called P1 and P2 in the following discussion), one should perform a cross to obtain F1 hybrid offspring. However, before proceeding to a second-generation cross, it is critical to determine the expression of the trait of interest in the F1 population. Figure 9.18 shows different examples of the potential results that might be obtained. If the pairs of alleles present at all "polygenetic" loci that distinguish P1 from P2 act in a strictly semidominant manner, the F1 population will show a mean level of expression halfway between the means of the two parental strains (example 3 in Figure 9.18). On the other hand, the F1 population may show a distribution that is indistinguishable from one parental strain or the other if there are strong dominant effects (example 1 in Figure 9.18). Finally, a likely result is the complex one with unequal allele strengths — but not strict dominance — that lead to a distribution differing from both parental strains, but with a mean value that is closer to one than the other (example 2 in the Figure 9.18). In fact, the F1 distribution can have a mean value that lies anywhere along the continuum between the two parental means. However, in all cases, the standard deviation around this mean value should be similar to that found with the parental strains, since the F1 population is always genetically homogeneous. 99
If the mean expression of the F1 population lies essentially halfway between that found with the two parental strains, then the backcross can be performed with either parent. Other criteria, such as reproductive performance, should be the deciding factors (Chapter 4 and Table 4.1). 100 However, if the mean F1 expression is closer to one parent (such as P1 in examples 1 and 2 shown in Figure 9.18), one should backcross F1 animals to the opposite parent (P2 in the example). As one can see from Figure 9.18, this choice will serve to minimize the degree of phenotypic overlap between the two "parents of the backcross" and will allow a more accurate identification of N2 animals with genotypes that match one parent or the other as discussed below.
It has been customary in mouse genetic studies to perform a backcross between an F1 female and a male from the chosen parental strain. The main advantage to backcrossing in this direction is the higher fecundity of F1 females that results from "hybrid vigor". However, as discussed in Sections 9.4.1 and 9.4.4.2, it may sometimes be more advantageous to cross the F1 male with an inbred female.
Once backcross (N2) progeny are obtained, they can be analyzed for expression of the trait of interest with the same protocol used to measure expression in the F1 and progenitor strain (P1 and P2) populations. When a sufficient number of N2 animals have been tested, the distribution of expression levels can be graphed out and compared to the distributions obtained with the F1 and P2 populations. The right hand side of Figure 9.19 shows examples of the idealized distributions that one would obtain upon analysis of a trait whose expression is determined through the additive effects of semidominant alleles at one, two, or three loci that contribute equally to expression levels.
Consider the trival case in which a trait that what was thought to be polygenic is actually controlled primarily by a single locus, A, having two
semidominant alleles A1 and A2. There are only two potential gentoypes in the N2 population obtained from
backcrossing to parent P2:
Next, consider the simplest case of polygenic inheritance with alleles at two major loci, A and B, that both have additive semidominant effects
on expression. In this case, the number of relevant N2 genotypes doubles from two to four:
In some experimental cases, when there is a sufficient distance between the mean values of expression of the two parents, it may be possible to actually obtain a triphasic distribution pattern with a shape and peak distribution similar to that shown in the middle right hand panel of Figure 9.19. A result of this type would be a sign that only two major additive loci were involved in the expression of the trait.
In most experimental situations, the distribution patterns obtained for the expression of a complex trait of interest in an N2 population are unlikely to show significant evidence of multiple phases and multiple peaks. Rather, the most likely distribution will be an undifferentiated continuum that extends across the range between and beyond the mean values of expression observed for the F1 and P2 parental populations. There are several factors that are likely to contribute to this tendency toward a monophasic distribution. First, with each increment in the number of loci having an effect on expression, there will be a doubling in the number of different genotypes that are possible in the N2 population. With just three loci, the number of genotypes will be eight. If alleles at all three loci show addititive semidominant effects, a distribution of the form shown in the bottom right hand panel of Figure 9.19 will be obtained. This nearly monophasic distribution results from the combination of only four subdistributions that correspond to separate genotypic classes. 101 As the number of genes involved grows beyond three, the possibility of seeing multiple distribution peaks that correspond to different genotypic classes is essentially nil.
For the purposes of genetic analysis, the most critical feature of polygenic, quantitative trait inheritance is the impossibility of correlating intermediate levels of phenotypic expression with particular genotypes at each of the segregating loci involved. This problem is clearly visible even in the idealized distributions of the three locus trait shown in the bottom panels of Figure 9.19. In this simple example, an N2 phenotype halfway between the means of the F1 and P2 parents could be caused by heterozygosity at any one or two of the three loci involved; thus, this halfway phenotype is almost useless in terms of providing marker linkage information. However, there will always be one or two portions of each N2 distribution that will have a high level of predictability for genotype at linked markers — the tails at one or both ends.
An N2 animal that shows an extreme level of phenotypic expression that is, in fact, within the normal range observed for one parental strain (either the F1 or P2) is likely to have the genotype of that parent at all of the segregating loci that distinguish the F1 and P2 parents. This means that a set of animals with the same extreme phenotype at one end of the N2 distribution will be likely to show a significant level of concordance with the same parental genotype at all markers that are closely linked to any one of the segregating trait loci. For example, imagine that one has chosen a subset of 20 N2 animals that most resemble the P2 parental strain in the expression of a trait and each animal within this set is typed for DNA markers that span the genome. A marker that is closely linked to any one of the trait loci will appear homozygous for the P2 allele in a significant majority of the animals of this subset. If possible, a second subset of animals could be collected that most resemble the F1 population; markers linked to the trait loci would appear heterozygous for the P1 and P2 alleles in a significant majority of the animals of this subset.
The strategy just described, known as "selective genotyping," provides the most highly efficient means for mapping polygenic loci (Soller, 1991). Phenotypic analysis is performed on the complete set of backcross animals which should typically number in the hundreds. This analysis allows the investigator to identify one or two smaller subsets of N2 animals with the greatest amount of genotypic information content. DNA typing is performed only on these smaller subsets, each of which can be pooled together into single composite samples as described in Section 9.4.4.4.
How does one decide what proportion of N2 animals to include in each extreme phenotypic subset when a continuum of expression levels is observed for the whole population? The answer is not simple. If one is too stringent, there may be too few animals to type and the power of the linkage test will suffer accordingly (Figure 9.13). However, if one is too lax, animals without a parental genotype at each critical locus will be included at a higher frequency (Figure 9.19). This will cause the level of discordance with truly linked markers to increase beyond the actual recombination fraction to a point that may fall beyond the level of significance shown in Figure 9.13. There will obviously be an optimal cutoff point, but it will be impossible to ascertain its position in advance without knowing how many segregating loci have a major effect on expression. As illustrated in Figure 9.19, as the number of loci grows, so does the phenotypic overlap between each completely parental genotypic class (indicated with dark lines) and its adjacent mixed genotypic class (indicated with lighter lines).
In a first round of analysis without prior information, a reasonable fraction of backcross animals to include within each extreme subset would be 10% (Soller, 1991). Since it is important to have at least 20 individual samples within each composite sample for DNA pooling, this would entail the inital phenotypic analysis of at least 200 backcross animals. With a sample size that is this small, the swept radius is quite modest (see Figure 9.13) and a large number of markers will be required to span the whole genome. If it is possible to pool together 30 or 40 samples, this will greatly improve the sweep of individual markers. Alternatively, if the DNA pooling method provides evidence of potential marker linkage, the results obtained upon analysis of individual samples in the two extreme classes (if there are two that can be formed) can be combined for greater statistical power.
The results obtained from the initial analysis of the 10% DNA pools will provide the investigator with a certain amount of information on the experimental direction that is best to follow. For example, if the initial analysis allows the identification of even one marker that shows 100% concordance within an extreme phenotypic class, it is likely that this class does not contain any animals with non-parental genotypes. Thus, it would be worthwhile to expand the extreme class to include a larger sample size to search more efficiently for markers linked to additional loci that affect trait expression. Furthermore, positive results with individual markers that fail to meet the most stringent requirements for significance could still be pursued through the typing of markers that are 10-20 cM removed and may be closer to a potential trait locus. If a trait locus is, indeed, present in the vicinity of the original marker, this strategy could yield closer markers that will show higher levels of concordance and significance. Finally, once QT loci have been defined, an investigator can return to the complete set of animals and type all of those not typed already for closely linked QT marker loci. This more comprehensive data set can be subjected to advanced non-parametric statistical methods, such as the Mann-Whitney U test 102 (available within most statistical software packages for desktop computers), in order to better understand the nature of the interactions among QT loci.