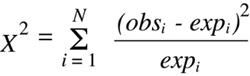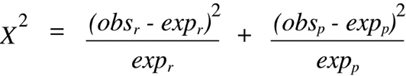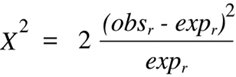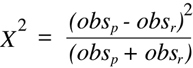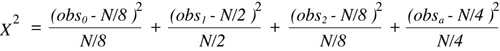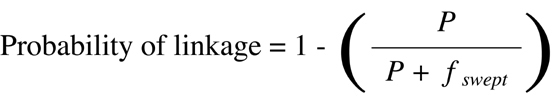9.1 DEMONSTRATION OF LINKAGE AND STATISTICAL ANALYSIS

9.1.1 Mapping new DNA loci with established mapping panels

When a new mouse locus has been defined at the DNA level, it can be mapped by three different approaches: somatic cell hybrid analysis, in situ hybridization, or formal linkage analysis. The first of these approaches is not applicable generally to the mouse because single chromosome hybrids have not been gathered together in a systematic way for the whole mouse genome. However, even in those cases where such hybrids exist, this type of analysis provides only a chromosomal assignment. The second approach — in situ hybridization — is more highly resolving than somatic cell hybrid analysis, but this protocol requires special expertise and the resolution is still less than that obtained routinely with linkage analysis. Both of these non-sexual mapping protocols have two advantages over all forms of linkage analysis. First, they do not require any prior knowledge of map positions for other loci. Second, they allow the mapping of non-polymorphic loci. Thus, in the early days of mouse molecular genetics, before many DNA markers had been placed onto the map, and before new methods for uncovering polymorphisms had been developed, both of these protocols served useful functions in the arsenal of general mapping tools.

Today, the method of choice for mapping a new locus defined at the DNA level will always be formal linkage analysis. There are two interrelated reasons for this. First, a whole genome mouse linkage map of very high density has been developed with thousands of polymorphic DNA markers already in place and new ones being added each month (Copeland et al., 1993). The second reason lies within the existence of various mouse "mapping panels" that have been established by a number of investigators at different institutions around the world.

A mapping panel is a set of DNA samples obtained from animals that carry random recombinant chromosomes produced within the context of a specific breeding scheme. The most widely used mouse mapping panels are of two specific types. One consists of representative DNA samples derived from each strain of a recombinant inbred (RI) set or group of RI sets. The approach to mapping with RI strains will be detailed in Section 9.2. The second type of widely used mapping panel contains samples derived from the offspring of an interspecific backcross between the two species, M. musculus and M. spretus. This approach will be discussed in Section 9.3. It is also possible to design mapping panels that are based on an intercross between two F₁ hybrid parents obtained in an interspecific or intersubspecific outcross between two different inbred strains (Dietrich et al., 1992).

The power of mapping panels lies within the database of information that is already available for a large number of previously typed loci in members of the same defined cohort of animals. The most useful panels have been typed for at least 200 independent DNA markers and, in fact, the most well-established panels have been typed for many more. In classical genetic terminology, this can be viewed as a multihundred point cross that provides linkage maps across the complete spans of all chromosomes in the genome.

Thus, the mapping of a new locus can be accomplished simply by genotyping each of the samples in the same cohort (or a subset thereof) for just the new locus of interest. It is never necessary to type more than one hundred animals in the initial analysis and, as discussed in Sections 9.2 and 9.4, with a well-characterized panel, one can usually obtain a map position with the typing of 50 or fewer animals. A single investigator can easily carry out such an analysis in less than a week's time with the use of either a PCR analysis or Southern blotting. The results obtained are entered into the database containing all prior mapping information on the panel and a computational algorithm is used to determine the location of the new locus within the already-established linkage map. Essentially, this is accomplished by searching for concordant segregation between alleles at the new locus and those at one or more loci that have been previously typed on the same panel. With a well-established mapping panel, a first-order map position will always be obtained. A discussion of the two most important classes of mapping panels — recombinant inbred strains and the interspecific backcross — will be presented in Sections 9.2 and 9.3 of this Chapter.

9.1.2 Anchoring centromeres and telomeres onto the map

As discussed in Section 5.2, all 21 chromosomes in the standard mouse karyotype (19 autosomes and the X and Y) are extremely acrocentric. Even with very high resolution light microscopy of extended prophase chromosomes, the centromere appears to lie at one end of each chromosome. Although there must be a segment of DNA containing at least a telomeric sequence that precedes the centromere, no unique sequence loci have ever been localized to this hypothetical segment. Thus, for all intends and purposes, one can view the genetic map of each chromosome as beginning with a centromere and ending with a telomere.

In the absence of centromere and telomere mapping information, a linkage map will be unanchored. As a result, the length of genetic material that lies beyond the furthermost marker at each end of the map will not be known. However, since both centromeres and telomeres are composed of repeated simple sequences that are shared among all chromosomes, their direct mapping requires special approaches.

9.1.2.1 Telomere mapping

All mammalian telomeres are composed of thousands of tandem copies of the same basic repeat unit TTAGGG (Moyzis et al., 1988; Elliott and Yen, 1991). Early sequence comparisons indicated that while the basic repeat unit was highly conserved, occassional nucleotide changes could arise anywhere within the large telomeric sequence present at the end of any chromosome. Elliott and Yen (1991) realized that one particular nucleotide change, from a G to a C in the sixth position of this repeat unit, would create a DdeI restriction site (CTNAG) that overlapped two adjacent repeats — [TTAGGC][TTAGGG]. In the absence of such a change, the enzyme DdeI would not cut anywhere inside a particular telomeric region which would remain intact within a restriction fragment of 20 kb or more in size. In contrast, one or more substitutions of the type described would allow DdeI to reduce a telomeric region into smaller restriction fragments that could be detected by probing a Southern blot with a labeled oligonucleotide (called TELO) consisting of five tandem copies of the consensus telomere hexamer (Elliott and Yen, 1991). To date, strain-specific telomeric DdeI RFLPs have allowed the inclusion of telomeres from six mouse chromosomes as segregating markers in linkage studies (Eicher and Shown, 1993; Ceci et al., 1994). More recently, another repeat sequence has been identified with a subtelomeric position in all mouse chromosomes (Broccoli et al., 1992). In the future, it may be possible to develop analogous strategies for mapping telomeres with this subtelomeric repeat as well.

9.1.2.2 Centromere mapping with Robertsonian chromosomes

Unfortunately, the satellite sequences present within all mouse centromeres are not amenable to the same type of mapping strategy just described. The problem is that each centromere contains about eight megabases of satellite sequences (Section 5.3.4), which is about 400 times larger than a telomere.

Consequently, base substitutions away from the consensus satellite sequence will be much more numerous; this will lead to whole genome Southern blot patterns, with any restriction enzyme, that are unresolvable smears.

So, how does one go about placing centromeres onto a linkage map? One approach is to mark the centromeres of individual homologs with a Robertsonian fusion (see Section 5.2). If a test animal is heterozygous for a particular Robertsonian chromosome, the segregation of the fused centromere can be followed in each offspring through karyotypic analysis. If the Robertsonian chromosome carries distinguishable alleles at linked loci, the recombination distance between the centromere and these linked loci can be determined by DNA marker typing.

Unfortunately, this approach is complicated by the finding that local recombination is suppressed in animals heterozygous for many Robertsonian chromosomes due to minor structural differences that interfere with meiotic pairing (Davisson and Akeson, 1993). Thus, the distance between the centromere and the nearest genetic locus is likely to be underestimated by this method.

9.1.2.3 Centromere mapping through secondary oocytes

A second approach to determining distances between centromeres and linked markers is based on the genetic analysis of large numbers of individual "secondary oocytes," which are the products of the first meiotic division. As shown in Figure 9.1, sister chromatids remain together in the same nucleus after the first meiotic division. Thus, in the absence of crossing over, the secondary oocyte will receive one complete parental homolog or the other, and would appear 034;homozygous" for all markers upon genetic analysis. However, if crossing over does occur, the oocyte will receive both parental alleles at all loci on the telomeric side of the crossover event. Thus, all telomeric-side loci that were heterozygous in the parent will also appear heterozygous in the oocyte, but all centromeric-side loci will remain homozygous. The fraction of individual oocytes that are heterozygous for a particular genetic marker will be twice the linkage distance that separates that marker from the centromere since only half of the haploid gametes generated from a double allele oocyte will actually carry the recombinant chromatid.

How does one go about determining the individual genotypes of large numbers of secondary oocytes? There are two basic protocols. The first to be developed was based on the clonal amplification of secondary oocytes within the form of ovarian teratomas (Eicher, 1978). Ovarian teratomas result from the parthenogenetic development of secondary oocytes into disorganized tumors that contain many different cell types. The inbred LT/Sv strain of mice undergoes spontaneous ovarian teratoma formation at a very high rate. This inbred strain in and of itself is not useful for oocyte-based linkage analysis since it is homozygous at all loci, but it is possible to construct congenic animals that are heterozygous for particular marker loci within an overall LT/Sv genetic background. In the cases reported, these congenic animals retain the high rate of teratoma formation associated with the parental LT/Sv strain (Eppig and Eicher, 1983; Artzt et al., 1987; Eppig and Eicher, 1988). This approach is tedious in that a different congenic line has to be developed to map centromeres on each chromosome, but there is every reason to believe that the results obtained are an accurate measure of centromere-marker linkage distances in female mice.

An alternative protocol for genotyping oocytes is based on DNA amplification (by PCR) rather than cellular amplification. The main advantage to this approach is that genotyping can be performed on oocytes derived from any heterozygous female (Cui et al., 1992). Thus, in theory, this approach could be used to position the centromere relative to any marker on any chromosome. However, in practice, PCR amplification from single cells is difficult, and there is a high potential for artifactual results — such as amplification from one DNA molecule but not its homolog.

9.1.2.4 Centromere mapping by in situ hybridization or Southern blots

A third approach to positioning centromeres on linkage maps is based on direct cytological analysis. This approach is possible because of the divergence in centromeric satellite DNA sequences that has occurred since the separation of M. musculus and M. spretus from a common ancestor ~3 million years ago (see Section 5.3 and Figure 2.2). In particular, the major satellite sequence in M. musculus is composed of a 234 bp repeat unit that is present in 700,000 copies distributed among all the centromeres. This same 234 bp repeat unit is only present in 25,000 copies spread among the centromeres in M. spretus (Matsuda and Chapman, 1991). The 28-fold differential in copy number can be exploited with the technique of in situ hybridization to readily distinguish the segregation of M. musculus centromeres from M. spretus centromeres in the offspring of an interspecific backcross. This approach has now been used to anchor all of the mouse chromosomes at their centromeric ends (Ceci et al., 1994). The only caveat to mention is the possibility that interspecific hybrids have a distorted recombination frequency in the vicinity of their centromeres.

A final possibility, that has yet to be validated, is the mapping of centromeres as RFLPs observed on Southern blots in the same manner as described for telomeres in Section 9.1.2.1. This approach may be possible with the use of a newly described repeat sequence that appears to be present in reasonable copy numbers adjacent to the centromeres of nearly every mouse chromosome (Broccoli et al., 1992).

9.1.3 Statistical treatment of linkage data

9.1.3.1 Testing the null hypothesis

Let us assume that two inbred strains of mice (B6 and C3H for example) carry distinguishable alleles (symbolized by b and c respectively) at each of two fictitious loci Xy1 and Gh3 as shown in Figure 9.2. An F₁ hybrid between B6 and C3H will be heterozygous at each locus with a genotype of:

Xy1^c/Xy1^b, Gh3^c/Gh3^b

If these two loci are linked on a single chromosome, the F₁ hybrid will have one homolog with the Xy1^c and Gh3^c alleles, and the other homolog with the Xy1^b and Gh3^b alleles. By definition, linkage means that the F₁ hybrid will produce a greater number of gametes carrying a parental set of alleles, either:

Xy1^b Gh3^b or Xy1^c Gh3^c

than a recombinant set of alleles, either:

Xy1^b Gh3^c or Xy1^c Gh3^b.

As discussed at length in Section 7.2, the actual distance that separates the two loci will determine the strength of their linkage in terms of the fraction of recombinant gametes.

If one could determine the haploid genotype (or haplotype) of each sperm produced by a C3H X B6 hybrid male, one would know for sure whether the two loci in question are linked. But with the typing of a finite number of progeny in an experimental cross, the answer is often not as clear. Let us say that 100 offspring from the F₁ hybrid have been typed to test for linkage between Xy1 and Gh3 with the result that 62 carry parental allele combinations and 38 carry non-parental allele combinations. Do these data provide evidence in favor of the hypothesis: "Xy1 and Gh3 are linked"?

Unfortunately, there is a problem with a general hypothesis that states "genes A and B are linked" in that there is no precise prediction of what to expect in terms of data from a breeding experiment. This is because linkage can be very tight so that recombination would be expected rarely, or linkage can be rather loose so that recombination would be expected frequently. Of course, the strength of linkage, if indeed the genes under analysis are linked, is unknown at the outset of the experiment. In contrast, there is a precise prediction of what to expect from the so- called "null hypothesis" of no linkage between genes A and B. The prediction of this null hypothesis is that alleles at different genes will assort independently leading to a 50:50 ratio of gametes with parental or recombinant combinations of alleles.

Thus, whenever geneticists wish to determine whether their data provide evidence for linkage (of any degree), what they actually do is ask the following question: are these data significantly different from what one would expect if the two loci were not linked? With this well-defined "null hypothesis", it becomes possible to apply a statistical test to determine whether the data actually observed are significantly different from the expected outcome for no linkage. In the example above, with the analysis of 100 offspring, the null hypothesis would lead to a prediction of 50 animals with a parental allele combination and 50 animals with a recombinant allele combination in comparison with the observed results of 62 and 38 respectively. Are these two sets of numbers significantly different from each other? If the answer is yes, this would suggest that the null hypothesis is false and that the two loci are indeed linked. On the other hand, if the observed data are not significantly different from those expected from the null hypothesis, the question of linkage will remain unresolved — the two loci may be unlinked, but it may also be possible that the loci are linked and there are simply not enough data to detect it.

9.1.3.2 A comparison of mouse linkage data and human pedigree data

Before launching into a discussion of the statistical treatment of linkage data, it is important to illuminate a critical difference between linkage analysis in the mouse and in humans. In nearly all cases of linkage analysis in the mouse, the parental combinations of alleles — the so-called phase of linkage — will be known with absolute certainty. In the example above, if we assume that the two loci in question are linked, we know that the Xy1^c and Gh3^c alleles will be present on one homolog and the Xy1^b and Gh3^b alleles will be present on the other homolog in the F₁ hybrid, as illustrated in Figure 9.2. With this information, we can tell immediately upon typing whether an offspring carries a parental or recombinant combination of alleles.

More often than not, the phase of linkage is not known with certainty in the analysis of human pedigrees. As a consequence, human geneticists are forced to employ more sophisticated statistical tools that evaluate results in light of the probabilities associated with each possible phase relationship for each parent in a pedigree (Elston and Stewart, 1971). These maximum likelihood estimation (MLE) analyses are always performed by computer and they lead to the determination of LOD score graphs which show the likelihood of linkage between two loci over a range of map distances (Morton, 1955). With most human pedigrees, it is impossible to count the actual number of recombination events that have occurred between two loci, and, as a consequence, it is impossible to determine even a most likely genetic distance separating two loci without the use of a computer. In contrast, all recombination events can be clearly detected in two of the three most common types of mouse breeding protocols — the backcross and RI strains — and with the intercross, all but a small percentage of recombination events can also be distinguished unambiguously (see Figure 9.4). With backcross and RI data in particular, linkage distance estimates can be easily determined by hand or with a simple calculator, and confidence limits around these estimates can be extrapolated from sets of tables (such as those in Appendix D).

9.1.3.3 The Chi-squared test for backcross data

The standard method for evaluating whether non-Mendelian recombination results are statistically significant is the "method of Chi-squared." Upon calculating a value for Chi-squared, one can use a look-up table to determine the likelihood that an observed set of data represents a chance deviation from the values predicted by a particular hypothesis. This determination can lead one to reject or accept the hypothesis that is being tested.

In its most general form, the Chi-squared statistic is defined as follows:

(Equation 9.1)



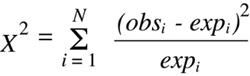
where there are n potential outcome classes, each of which is associated with an observed number (obs_i) that is experimentally determined and an expected number (exp_i) that is calculated from the hypothesis being tested. It is obvious from a quick examination of Equation 9.1 that as the differences between observed and expected values become larger, the calculated value of Chi-squared will also become larger. Thus the Chi-squared value is inversely related to the goodness of fit between the experimental results and the null hypothesis being tested, with a Chi-squared value of zero indicating a perfect fit. As the value of Chi-squared grows larger and larger, the likelihood that the experimental data can be explained by the null hypothesis becomes smaller and smaller.

Consider the case of a backcross with the (B6 X C3H) F₁ hybrid described above to analyze the possibility of linkage between the fictitious loci Xy1 and Gh3. In terms of these two loci, the F₁ hybrid can produce four types of meiotic products which will engender four experimental outcome classes ( Figure 9.2). If one makes the a priori assumption that the two parental classes represent different manifestations of the same outcome of no recombination, and the two other classes represent, for all practical purposes, reciprocal products of the same recombination event, then the data can be reduced in complexity to a set of just two outcomes — parental or recombinant. ⁶⁹ In this case, the Chi-squared statistic becomes:

(Equation 9.2)



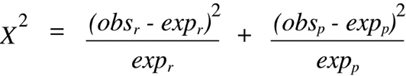
where the r subscript indicates recombinant and the p subscript indicates parental.

Whenever the Chi-squared test is used to analyze data obtained from a backcross and the null hypothesis is one of no linkage, a further simplification of Equation 9.2 can be accomplished. In this case, the expected values for parental and recombinant classes will both be equivalent to half the total number (N) of offspring typed (which is the sum of the two observed values). Furthermore, the two observed values will both differ from the expected value by the same absolute number, and the square of each difference will yield the same positive value. Thus, the two terms in Equation 9.2 can be combined to form:

(Equation 9.3)



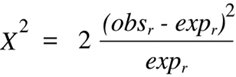
Equation 9.3 can be simplified even further by substituting each appearance of exp_r with the equivalent expression (obs_p + obs_r)/2. The form of the equation that is so derived contains only the two experimentally obtained values as variables:

(Equation 9.4)

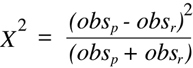
In plain English, Equation 9.4 can be read as "square the difference, divide by the sum",; and this simple calculation can often be performed through mental calculations alone. ⁷⁰

Now we can return to our example from above with 62 parental and 38 recombinant allele combinations and use Equation 9.4 to determine the appropriate Chi-squared value. The difference between the numbers in the two observation classes (62 - 38 = 24) is squared to yield 576, and this value is divided by the total size of the sampled population (100) to yield 5.76.

One more piece of information is required before it is possible to translate a Chi-squared value into a measurement of significance — the number of "degrees of freedom" (df) associated with the particular experimental design. The "degrees of freedom" is always one less than the total number of potential outcome classes (df = n - 1). The rationale for this definition is that it is always possible to determine the number of events that have occurred in the any one class by subtracting the sum of the events in all other classes from the total size of the sample set. In the backcross example under discussion, we have defined two potential outcome classes: recombinant and parental. Knowing the number in either class, along with the total sample size, provides the number in the other class. Thus, the number of degrees of freedom in this case is one.

With a Chi-squared value and the number of degrees of freedom in hand, one can proceed to a Chi-squared probability look-up table such as the one presented in Table 9.1. This table shows the Chi-squared values that are associated with different "P values." A P value is a measure of the probability with which a particular data set, or one even more extreme, would have occured just by chance if the null hypothesis were indeed true. To obtain a P value for the data set in the example under discussion, we would look across the row associated with one degree of freedom to find the largest Chi-squared value that is still less than the one obtained experimentally. In this case, this procedure yields the Chi-squared value of 3.8. Looking up the column from this Chi-squared value, we obtain a P value of 0.05. ⁷¹ We have now reached the final goal of our statistical test for significance.

In this hypothetical example, our statistical analysis indicates that the data obtained would be expected to occur with a frequency of less than 5% if the two loci were not linked. However, is this result significant enough to prove linkage? To answer this question, it is very important to understand exactly what it is that the Chi-squared test and its associated P value do and what they do not do. The outcome of a Chi-squared test cannot prove linkage or the absence thereof. It just provides one with a quantitative measure of significance. What is a significant result? Traditionally, scientists have chosen a P value of 0.05 as an arbitrary cutoff. But with this choice, one will conclude falsely that linkage exists in one of every twenty experiments conducted on loci that are, in fact, not linked! As discussed below in Section 9.1.3.6, the interpretation of a Chi-squared value in modern genetic experiments that look simultaneously for linkage between a test locus and large numbers of genetic markers is subject to further restrictions that result from the application of Bayes' theorem.

9.1.3.4 The Chi-squared test for intercross data

It is instructive to consider the application of the Chi-squared test to a breeding protocol with more than two potential outcome classes. The most relevant example of this type is the intercross between two F₁ hybrid animals that are identically heterozygous at two loci with a genotype of A/a, B/b. Figure 9.3 illustrates the different types of F₂ offspring genotypes that are possible in the form of a Punnett square. In the absence of linkage between A and B one would expect each of the sixteen squares shown to be represented in equal proportions among the F₂ progeny. If one compares the actual genotypes present in each square, one finds that there is some redundancy with only nine different genotypes in total. These are as follows (with their relative occurrences in the Punnett Square shown in parenthesis):

• A/A, B/B (1)
• a/a, b/b (1)
• A/a, B/b (4)
• A/A, B/b (2)
• A/a, B/B (2)
• A/a, b/b (2)
• a/a, B/b (2)
• A/A, b/b (1)
• a/a, B/B (1)

• A/A, B/B
• a/a, b/b

• A/A, B/b
• A/a, b/b
• a/a, B/b
• A/a, B/B

• A/A, b/b
• a/a, B/B

• zero recombinants — 1/8
• single recombinants — 1/2
• double recombinants — 1/8
• ambiguous (zero or two recombinants) — 1/4

With this information, it becomes possible to set up a Chi-squared test to evaluate the evidence for linkage between two segregating loci typed among the progeny of an (F₁ X F₁) intercross. The special Chi-squared equation for the intercross takes the following form:

(Equation 9.5)



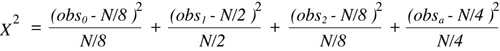
where the subscript in each observational class indicates the number of recombination events (obs_a is the ambiguous class) and N is the total number of F₂ progeny typed. An comparison of the experimentally determined Chi-squared value with the critical values shown in the df = 3 row of Table 9.2 will allow a determination of a corresponding P value.

9.1.3.5 Limitations and corrections in the use of the Chi-squared test

The Chi-squared test does have some limitations in usage. First, it cannot be applied to very small data sets, which are defined as those in which 20% or more of the outcome classes have expected values that are less than five (Cochran, 1954). With this rule, it is possible to set minimum sample sizes required for the analysis of backcross data at 10, and F₁ X F₁ intercross data at 40. In actuality, a backcross or RI data set must include at least 13 samples to show significance in the case of no recombinants (based on the Bayesian correction described below). Furthermore, when the sample size is below 40 (in cases of one degree of freedom only), a more accurate P value is obtained if one includes the Yates correction for small numbers. This is accomplished by subtracting 0.5 from the absolute difference between observed and expected values in the numerator of Equation 9.3.

A final point is that Chi-squared analysis provides a general statistical test for significance that can be used with many different experimental designs and with null hypotheses other than the complete absence of linkage. As long as a null hypothesis can be proposed that leads to a predicted set of values for a defined set of data classes, then one can readily determine the goodness of fit between the null hypothesis and the data that are actually collected.

9.1.3.6 A Bayesian correction for whole genome linkage testing

If one has reason to believe from other results that two loci are just as likely to be linked as not, then the P value obtained with the Chi-squared test can be used directly as an estimate of the probability with which the null hypothesis is likely to be true, and subtracting the P value from the integer one provides a direct estimate of the probability of linkage. However, when a previously unmapped locus is being tested for linkage to a large number of markers across the genome, there is usually no a priori reason to expect linkage between the new locus and any one particular marker locus. If we assume a particular experimental design such that linkage is detectable out to 25 cM on both sides of an unmapped locus ⁷² and a total genome length of 1,500 cM, then the fraction of the genome in linkage with the novel locus will be (25 + 25)/1,500 ~= 0.033. In other words, out of 100 markers distributed randomly across the genome, one would expect only 3.3 to actually be in linkage with any particular test locus. But, if one accepts a P value of 0.05 as providing evidence for linkage, then 5% of the unlinked 97 loci — or an additional ~5 loci — will be falsely considered linked according to this statistical test. As a consequence, the expected number of false positives — five — is larger than the expected number of truly linked loci — 3.3. Thus, of the 8.3 positive markers expected, only 3.3 would be linked, and this means that a P value of 0.05 has only provided a probability of linkage of 40%. This situation is clearly unacceptable.

The logical approach just discussed is referred to as Bayesian analysis after the statistician who first suggested that prior information on the likelihood of outcomes be included in calculations of probabilities. One can generalize from the example given to obtain a Bayesian equation for converting any P value obtained by Chi-squared analysis of recombination data into an actual estimate of the probability of linkage: ⁷³

(Equation 9.6)



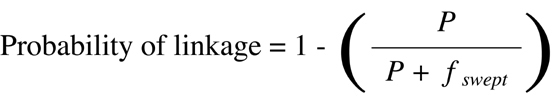
where P is the P value obtained by Chi-squared analysis and f_swept is the fraction of the genome over which linkage can be detected based on the power of the genetic approach used. ⁷⁴ Solutions to Equation 9.6 for some critical P values and genomic distances are given in Table 9.2. Of interest are the P values required to provide evidence for linkage with 95% probability. So long as the experimental design allows detection of linkage out to 15 cM, one can use a cutoff P value of 0.001 as evidence for linkage between any two loci. In accepting linkage at P < 0.001, one is actually setting a limit for accepting less than one false positive result for every 20 true positive results. Later in this chapter, the Bayesian approach is used to calculate cutoff values for the demonstration of linkage with 95% probability in the case of RI strain data (Figure 9.5) and backcross data (Figure 9.13).